مامدى مصداقية الأبحاث العلمية؟

مدخل

مؤخرًا، بدأ عدد من الباحثين في مشروع بحثي ضخم جدًا وهو محاولة لإستنساخ أو إعادة أكثر من ٢٥٠ دراسة وبحث علمي في علم النفس لاختبار مدى مصداقية النتائج التي حصل عليها الباحثون، بدأ المشروع في عام ٢٠١١ وانتهوا من جمع البيانات في نهاية ٢٠١٤، ومؤخرًا تم نشر النتائج المبدئية لأول دفعة من الدراسات وعددها ١٠٠ دراسة علمية منشورة في أكبر ثلاث مجلات علمية في مجال علم النفس، الباحثون حاولوا أن يلتزموا بكل المتغيرات المعطاة لكل دراسة منشورة لمعرفة ما مدى مصداقية النتائج التي توصلوا إليها، ومدى قابلية الحصول على نفس النتيجة، ٩٧٪ من الـ ١٠٠ دراسة حصلت على دلالة إحصائية عالية (p<0.05)، فقط ٣٦٪ أظهرت نتائج ذات دلالة إحصائية عالية (p<0.05)، بينما ٤٧٪ من الدراسات أظهرت “حجم تأثير” قريب من حجم التأثير الذي ظهر في الدراسة الأصلية (وقع في فترة ثقة = 95%).

مالذي حدث بالضبط؟ إذا كانت الدراسات السابقة خرجت بدلالة إحصائية عالية،أليس من المفترض أن نستخلص أن ما توصلت له الدراسة هو حقيقي ولم يكن فقط محظ الصدفة؟ وبما أن القيمة الإحتمالية p أقل من 0.05، ألا يعني هذا بأن النتائج صحيحة بنسبة ٩٥٪ ؟ في الحقيقة لا! ولكن الخطأ وقع في فهم القيمة الإحتمالية p، بل أن مجلة علم النفس الإجتماعي النظري والتطبيقي (Journal of Basic and Applied Social Psychology) حظرت على الباحثين استخدام القيمة الإحتمالية p كمعيار لمصداقية البحث وأهميته!

أين المشكلة بالضبط، هل أن القيمة الإحتمالية p فشلت وأصبحت عديمة النفع؟ أم في استخدام القيمة الإحتمالية p والإستدلال منها على المصداقية؟ للإجابة على هذا السؤال، سأظطر أن أشرح القيمة الإحتمالية وعلاقتها بالمصداقية في الأبحاث العلمية بشكل مبسط قدر المستطاع.

القيمة الإحتمالية ومستوى الدلالة

القيمة الإحتمالية والتي يُرمز لها بالحرف p، هي عبارة عن رقم بين 0 و 1 يقدّر ما إذا كانت النتيجة التي حصلت عليها كانت صدفة! أي أنه كلما صغر الرقم كلما كانت نتيجتك حقيقية ولم تكن بالصدفة، هذا فقط كل ماتقوله القيمة الإحتمالية، باختصار تربط النتيجة بإحتمالية المصادفة، ويُسمى هذا الإختبار بإختبار الفرضية الإحصائية، ويتم مقارنة هذا الرقم برقم آخر يسمى “مستوى الدلالة“، ويعتبر مثل المرجع الإحصائي لرفض أو قبول الفرضية، فعلى سبيل المثال الدراسات المنشورة في العلوم النظرية مثل علم النفس تعتمد على الرقم 0.05 في الإستدلال على أهمية البحث، فإذا كانت القيمة الإحتمالية p أقل من هذا الرقم فهذه إشارة أولى “فقط” إلى أن نتيجة هذا البحث بناءًا على العينات التي حصل عليها لم تكن صدفة!

المشكلة تبدأ عندما يتم تفسير  نتائج الأبحاث العلمية بناءًا على هذا الرقم فقط من قبل الباحث أو المراجع للبحث، حيث أن القيمة الإحتمالية p لا تُجيب على سؤال الباحث الحقيقي ولا تدعم موقفه، بل أنها فقط تُشير إلى أن العيّنة أو النتيجة التي حصل عليها هي نتيجة لم تخضع للصدفة، ويجب عليه أن يجري عدد من الإختبارات الأخرى لمعرفة حجم التأثير وغير من الإختبارات التي ستساعده على التأكد من وجود تأثير حقيقي، أي أن نجاح العيّنة في إختبار القيمة الإحتمالية ماهو إلا إشارة مبدئية إيجابية على أن العيّنة قد تحتوي على نتيجة حقيقية.

مثال نظري

لنضرب مثالًا على ذلك، لو كان هناك باحث إقتصادي يحاول أن يحدد ما إذا كان استخدام الكهرباء للحي الذي يتكون من عدد كبير من المنازل قد تغير عن السنة الماضية التي كان متوسط فاتورة الكهرباء 260 دولار، قام الباحث باختيار ٢٥ منزل بشكل عشوائي وقام بتسجيل مبلغ الفواتير الكهربائية شهريًا لهذه السنة، وحسب المتوسط لكل السنة ليحصل على 330.6 دولار (مصدر المثال)، لكي نختبر ما إذا كان المتوسط الجديد هو رقم حصل عليه الباحث بالصدفة أو لا، يجب أن ننظر إلى الرسم البياني للتوزيع العشوائي، والذي تم رسمه باستخدام أدوات إحصائية تعتمد على متوسط السنة السابقة، وعدد العينات التي جُمعت ومدى التباين فيها.

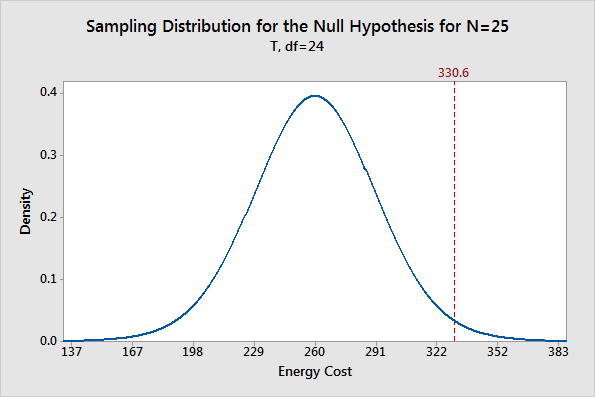هذه الرسمة توضح التوزيع العشوائي لفاتورة الكهرباء في السنة السابقة، حيث أن المتوسط هو 260 دولار، والرسمة توضح إحتمالية مبلغ الفاتورة للسنة الحالية، على سبيل المثال إحتمالية أن تكون فاتورة السنة الحالية 260دولار هي 40٪ تقريبًا، يعني بشكل عام نستطيع القول أن الرسم البياني يشير إلى أن يكون المبلغ بين 167 و 352 بإحتمالات متفاوتة.

إختبار الفرضية

الآن دعونا نحاول أن نقوم بعملية إختبار فرضية (Hypothesis Test)، وهذا إختبار يستخدمه الباحث للتأكد من دقة معلومات معينة عن مجتمع معين، في هذا المثال نحاول أن نختبر قيمة متوسط فاتورة الكهرباء، وبهذه الإختبار سنحاول التأكد ما إذا كان هناك تغيرات أثّرت على تغير قيمة المتوسط عن السنة السابقة، وهناك فرضيتين تخضع لهذا الإختبار:

1. فرضية العدم (Null Hypotheses) ويرمز لها بالرمز H_o: تفترض أن متوسط فاتورة الكهرباء للسنة الحالية يساوي متوسط السنة السابقة ولايوجد أي إختلاف،
2. الفرضية البديلة (Alternative Hypotheses)، ويرمز لها بالرمز H₁:وتُقبل في حال تم رفض فرضية العدم H_o: أي أنها تقر على أن هناك إختلاف مابين متوسط السنة الحالية والسنة السابقة.

خطأ النوع الأول وخطأ النوع الثاني

خطأ النوع الأول وخطأ النوع الثاني (Type I and type II errors)، وهي مقاييس لإختبار الفرضية (فرضية العدم والفرضية البديلة)، وهناك نوعين كما يشير العنوان:

1. خطأ النوع الأول: عندما يتم رفض “فرضية العدم” عندما تكون صحيحة!
2. خطأ النوع الثاني: عندما يتم قبول “فرضية العدم” عندما تكون خاطئة!

ولكي تفهم أنواع الخطأ بسهولة سأربطها بالمثال، نقع في الخطأ الأول عندما نرفض أن متوسط فاتورة الكهرباء للسنة الحالية يساوي السنة السابقة والصحيح أنه إحصائيًا الفواتير متساوية، والخطأ الثاني نقع فيه عندما نقبل أن متوسط فاتورة الكهرباء للسنة الحالية يساوي السنة السابقة والواقع أن الفواتير غير متساوية.

هل تذكرون مستوى الدلالة الذي ناقشته قبل قليل؟ هناك علاقة مباشرة بينها وبين خطأ النوع الأول، لذلك تُعرّف مستوى الدلالة بأنها “أقصى احتمال يمكن تحمله من الخطأ الأول”. ذلك يعني أنناسنحدد أقصى خطأ من النوع الأول ونستخدمه ليكون مستوى الدلالة، وهذا أمر مهم جدًا ولذلك تجد أن مستوى الدلالة المستخدم في الفيزياء لإستدلال على وجود جُسيم  (p=0.003) أقل بكثير من مستوى الدلالة المستخدم في علم النفس (p=0.05) وذلك للتأكد من صحة الإستدلال وأهمية عدم الوقوع في خطأ، إضافة إلى أن عدد المحاولات (العيّنات) عادة تكون أعلى بكثير في الفيزياء منها في العلوم النظرية وإحتمالية الوقوع في الخطأ وارده ولذلك تم تقليل مستوى الدلالة وذلك للتأكد من أن الجُسيم الذي تم اكتشافه هو جُسيم حقيقي والعيّنات لم تخضع لعامل الصدفة، تذكرون جُسيم بوزون؟ كانت القيمة الإحتمالية التي وجدها العلماء (p=0.0000003) وهي أقل بكثييير من المستوى الدلالي المطلوب مما يؤكد على أن العيّنات التي وجدوها ترفض فرضية العدم!

في القسم التالي ستتضح الصورة بشكل أفضل عندما نستخدم أكثر من مستوى دلالة لمعرفة الفرق.

إختبار المثال

تلخيص مبسط لما وصلنا إليه إلى الآن، عندنا متوسط السنة الحالية ومتوسط السنة الماضية ونريد أن نُجري إختبار فرضية، ونستطيع إما أن نختبر فرضية العدم أو الفرضية البديلة لأن نتيجة إحداهما عكس نتيجة الآخر، لنختار فرضية العدم والتي ستجعل من فرضية الباحث أن تكون “لايوجد هناك أي فرق بين متوسط إستخدام الكهرباء بين السنة الماضية والسنة الحالية” (فرضية العدم)!

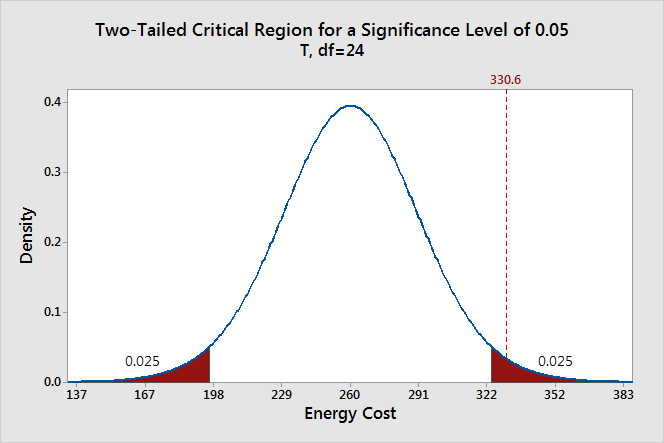
لنفترض أن مستوى الدلالة = 0.05 ، الرسمة البيانية التالية ستظلل ذيل التوزع العشوائي لآخر 0.05

نشاهد من الرسمة البيانية أن المتوسط الحسابي يقع في الجزء المظلل مما يعني أن القيمة الإحتمالية للمتوسط أقل من المستوى الدلالة p=0.05!

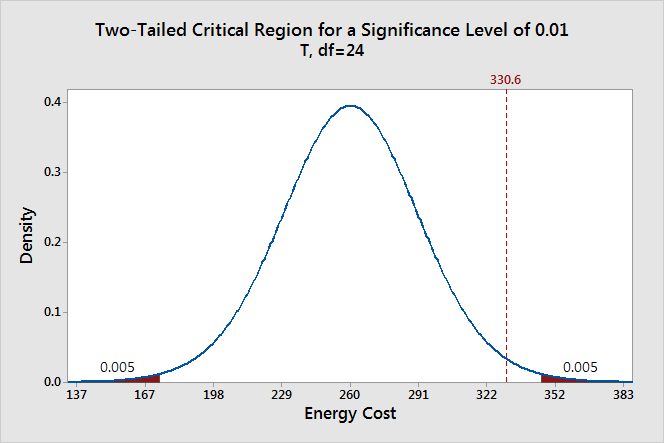
ولكن ماذا لو استخدمنا مستوى دلالة أقل من ذلك، لنستخدم p=0.01 سيظهر لنا الرسم البياني التالي:

سنجد أن المتوسط الحسابي لايقع في الجزء المظلل مما يعني أنه القيمة الإحتمالية له أكبر من مستوى الدلالة 0.01 ، وذلك لأن القيمة الإحتمالية للمتوسط بالضبط هي 0.01556

“القيمة الإحتمالية” لاتعني “إحتمالية الخطأ”

أكبر خطأ يقع فيه معظم الناس، بل حتى المجلات والمواقع العلمية، هو تفسير القيمة الإحتمالية p وكأنها إحتمالية حدوث الخطأ، فتجد البعض عندما يفسّر تأثير معيّن تم إكتشافه من قبل دراسة علمية حصلت على قيمة إحتمالية أقل من p=0.05، بأن الدراسة تقول أن التأثير صحيح بنسبة ٩٥٪ وهذا غير صحيح البتة كما وضحت في هذا المقال، حيث أن الإعتماد على القيمة الإحتمالية فقط لايكفي، لأنها لا تدل على إحتمالية حدوث التأثير وإنما تستنتج أن التأثير الذي تم إكتشافه من العيّنة المدروسة.

ولتوضيح أهمية عدم الإعتماد على القيمة الإحتمالية فقط وكذلك لتفسير عدم قدرة مشروع إستنساخ الدراسات على الحصول على نفس نتائج الدراسات السابقة، سأفصّل في موضوع إحتمالية الخطأ وعلاقته بالقيمة الإحتمالية، حيث قام باحث يُدعى “David Colquhoun” بدراسة تفصيلية لهذا الموضوع ولتقييم هذه العلاقة ووجد أن إستخدام مستوى دلالة = 0.05 يعني أن هناك على الأقل إحتمالية خطأ 30%، أي أن إحتمالية نجاح إستنساخ دراسة إعتمدت مستوى الدلالة 0.05 ضئيل ويصل في كثير من الأحيان إلى 50% ولا يقل عن 30٪! وهناك تفاصيل رياضية تشرح كيف استطاع الباحث تقدير إحتمالية الخطأ من القيمة الإحتمالية يمكنك الرجوع لها في الدراسة. علمًا أن هناك أكثر من دراسة استخدمت طرق إحصائية ورياضية مختلفة وتوصلت لنفس النتيجة مما يؤكد صحة هذه العلاقة.

متى تكون نتائج الدراسة مقنعة؟

إن نتائج مشروع إستنساخ الدراسات العلمية لا تدعو إلى سحب الثقة من الدراسات العلمية، وإنما تشير أهمية إستنساخ أي دراسة علمية للتأكد من صحة نتائجها، إضافة إلى أنها ساعدت في وضع خطط وتوجيهات لتصميم أفضل الدراسات وتقليل مصادر الأخطاء قدر الممكلن، ولقد لخص الباحث النقدي “Steven Novella” في مقالته أربع نقاط يجب أن تتواجد في أي نتيجة علمية لكي نقتنع بصحتها:

1. تصميم صارم للدراسة العلمية: ويقصد بأن تقوم الدراسة على شروط وضوابط معتمدة وأن يتم تحديد عدد الأشخاص ومستوى الدلالة المعتمد قبل بداية الدراسة.
2. نتائج ذات دلالة إحصائية: بالنظر إلى القيمة الإحتمالية p بالضبط، وعدم اعتماد دلالات عامة مثل “هذه الدراسة توصلت لقيمة إحتمالية أقل من 0.05”!
3. حجم التأثير يجب أن يكون جوهري: ويعني أن التأثير الذي تمت دراسته يجب أن يكون كبير نسبيًا، فلو أن هناك دراسة توصلت إلى أن العلاج “بعشبة ما” يساعد على تخفيف ربع كيلو كل ثلاث أشهر، فطبعًا هذا تأثير ضعيف جدًا وقد يكون نتيجة أي شيء آخر وليس بالضرورة استخدام هذه العشبة!
4. إستنساخ الدراسة بشكل مستقل: وهو إعادة الدراسة من قبل مجموعة بحثية مستقلة عن المجموعة التي قامت على الدراسة الأصلية للتأكد من صحة النتائج.

خاتمة

أعتذر عن طول المقالة، ولكن اضطررت أن أتطرق لكثير من التفاصيل الرياضية والإحصائية بعيدًا عن أي معادلات رياضية لكي يستوعبها القارئ، أتمنى أن تكون استفدت من هذه المقالة، وأن تكون حذرًا في تصديق أي نتائج مبنية على دراسة علمية قبل أن تتأكد من أنها تحتوي على كل هذه العناصر الأربعة، فالإعتماد على أحدها لن يكون كافيًا للإقتناع أو إعتماد نتائجها.